Ước số là một trong những khái niệm quan trọng trong kiến thức toán học lớp 6. Có rất nhiều bài tập vận dụng kiến thức về nó. Vậy nên hãy hãy cùng chúng tôi đi tìm hiểu ước số là gì? Cách tìm ước chung lớn nhất như thế nào trong nội dung dưới đây nhé!
Tóm tắt
Tìm hiểu về ước số
Khái niệm ước số
Ước số là gì? Ước số hay là ước được hiểu một cách đơn giản thì nếu có một số tự nhiên a chia hết cho số tự nhiên b, thì ta nói b chính là ước số của a. Hay có thể phát biểu cách khác là một số tự nhiên là ước số khi một số tự nhiên khác chia hết cho nó.
Kí hiệu của ước là: Ư(a)
Ví dụ: 4 chia hết cho 1, 2, 4 => Vậy {1;2;4} là ước của 4.
Được viết là: Ư(4)={1;2;4}
Ước số nguyên dương và ước số nguyên âm

Đầu tiên ta cần nhớ lại số nguyên dương và số nguyên âm. Số nguyên dương là các số tự nhiên bao gồm các số lớn hơn không. Còn số nguyên âm là số tự nhiên nhỏ hơn 0, được biểu diễn với dấu trừ đằng trước.
Vậy ước nguyên dương là gì? Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói b là ước của a. Trong đó a > 0
Còn ước nguyên âm được hiểu là: Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói b là ước của a. Trong đó a <0.
Ước số chung
Định nghĩa ước số chung
Ước chung là gì? Ước số chung của hai hay nhiều số là ước chung của tất cả các số đó.
Định nghĩa cách khác thì x là ước chung của a và b, nếu a chia hết cho x và b chia hết cho x.
Công thức: x € ƯC (a, b) nếu a ÷ x và b ÷ x
hay x € ƯC (a, b, c) nếu a ÷ x, b ÷ x và c ÷ x
Ví dụ 1:
2 chia hết cho 2 và 1
4 chia hết cho 2 và 1
6 chia hết cho 2 và 1
=> 2 và 1 chính là ước chung của 2, 4, 6
Ví dụ 2:
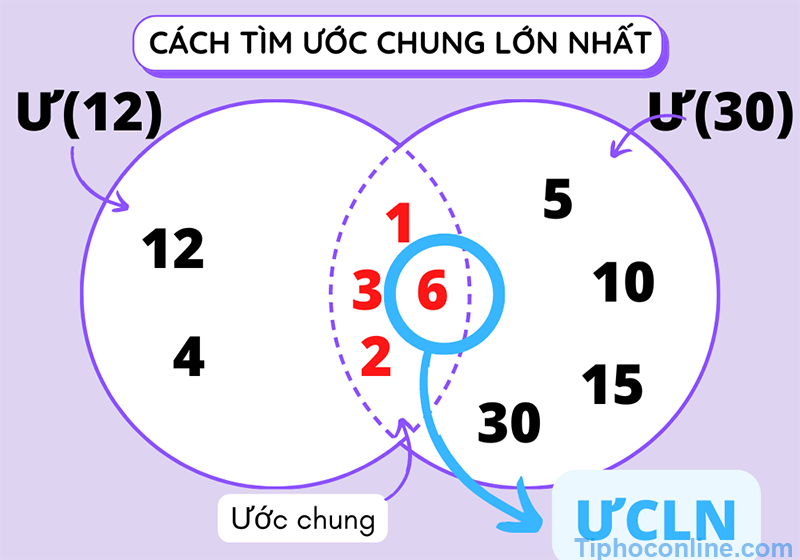
Ư(12) = {1, 2, 3, 4, 6, 12}
Ư(30) = {1, 2, 3, 5, 6, 10, 15, 30}
=> ƯC(12, 30) = {1, 2, 3, 6}
Ước số chung lớn nhất và nhỏ nhất
-
Ước số chung lớn nhất
Ước chung lớn nhất là gì? Ước số chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước số chung của các số đó.
Kí hiệu: Ước chung lớn nhất của số a, b được kí hiệu là: ƯCLN(a,b)
Ví dụ: Ta có Ư(6) = {1, 2, 3, 6}, Ư(12)={1, 2, 3, 4, 6, 12}
Vậy ước chung của 6 và 12 là: ƯC(6,12) ={1, 2, 3, 6}
Mà 6 là số lớn nhất trong tập hợp các ước chung của 6 và 12 nên ƯCLN(6,12) = 6
-
Ước chung nhỏ nhất
Ước chung nhỏ nhất của hai hay nhiều số là số bé nhất trong tập hợp các ước số chung của các số đó. Tuy nhiên với tất cả các số nguyên thì đều chia hết cho 1 và chính nó. Vậy mọi số khác 0 thì ước chung nhỏ nhất của chúng là 1.
Kí hiệu: Ước chung nhỏ nhất của số a, b được kí hiệu là ƯCLN(a,b)
Hướng dẫn cách tìm ước chung lớn nhất và nhỏ nhất
-
Cách tìm ước chung lớn nhất
Để tìm ước chung lớn nhất của một số ta thực hiện theo ba bước sau:
Bước 1: Đầu tiên phân tích số đã cho ra thừa số nguyên tố.
Bước 2: Tìm ra các thừa số nguyên tố chung.
Bước 3: Mỗi thừa số lấy số mũ nhỏ nhất của các thừa số chung rồi tính tích của nó. Kết quả ƯCLN cần tìm chính là tích đó.
Xem thêm:
- Số chính phương là gì, định nghĩa, tính chất và dấu hiệu
- Mốt của dấu hiệu là gì, cách tìm mốt của dấu hiệu
Các bài tập liên quan đến ước số
Để hiểu rõ hơn về ước chung lớn nhất và cách tìm ước chung lớn nhất thì các bạn hãy cùng chúng tôi giải các dạng bài tập dưới đây nhé!
Bài 1: Ước của 0 là gì?
Lời giải: Số 0 không phải là ước của bất kỳ số nguyên nào.
Bài 2: Tìm tập các ước số của 12
Lời giải: Số 12 chia hết cho các số ±1; ±2; ±3; ±4; ±6; ±12
Vậy tập hợp các ước số của 12 là: Ư(12) = {±1; ±2; ±3; ±4; ±6; ±12}
Bài 3: Hãy tìm ước chung lớn nhất của 2 số 14 và 28. (Biết các phần tử của ước ∈ Z+)
Lời giải: Cách tính ước chung lớn nhất là đầu tiên ta phân tích ra thừa số nguyên tố của hai số 14 và 28 như sau:
14 = 2 x 7
28 = 2 x 2 x 7
Ta có các thừa số nguyên tố chung là 2 và 7
Vậy ước chung lớn nhất của 2 số 14 và 28 là: 2 x 7 = 14
Được viết: ƯCLN(14,28) = 14
Bài 4: Tìm ước chung của 24 và 30, và ước chung lớn nhất là bao nhiêu? (Biết các phần tử của ước ∈ Z+)
Lời giải: Tìm ước của từng số ta có
Ư(24) = {1, 2, 3, 4, 6, 12, 24}
Ư(30) = {1, 2, 3, 5, 6, 10, 15, 30}
=> Ước chung của 24 và 30 là: ƯC(24,30) = {1, 2, 3, 6}
Trong các ước chung của 24 và 30 ta thấy 6 là ước lớn nhất. Do đó: ƯCLN(24,30) = 6
Bài 5: Tìm ước chung của 36 và 120 và chỉ ra ước chung lớn nhất của chúng. (Biết các phần tử của ước ∈ Z+)
Lời giải: Cách tìm ước chung thì đầu tiên ta tìm ước của từng số:
Ư(36) = {1, 2, 3, 4, 6, 9, 12, 18, 36}
Ư(120) = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}
Trong các ước của 36 và 120 ta thấy có các ước chung là: 1, 2, 3, 4, 6, 12
=> Vậy ƯC(36, 120) = {1, 2, 3, 4, 6, 12}
Mà trong số các ước chung thì 12 là ước lớn nhất nên ƯCLN(36, 120) = 12
Bài 6: Tìm hai ước của 15 có tổng bằng -4. (Biết các phần tử của ước ∈ Z)
Lời giải: Vì ước của 15 thuộc Z nên ta có:
Ư(15) = { -5, -3, -3, 1, 3, 5}
Theo đề bài cho thì tổng 2 ước cần tìm bằng – 4 => Vậy hai ước số cần tìm là: -5 và 1
Tạm kết: Vậy là chúng ta đã tìm hiểu lại kiến thức về ước chung lớn nhất thật kỹ càng qua các chia sẻ trên. Qua đó các em sẽ biết cách tìm ước chung lớn nhất của 2 hay nhiều số. Hãy vận dụng tốt các khái niệm cũng như công thức để giải bài tập cho thật chính xác nhé!




